递归算法分析方法总结
Date: 02 Aug 2015
之前在看《算法导论》这门网络公开课时,里面有介绍到3种分析递归算法的方法。当时觉得理解的挺清楚的,但是最近再回想起来有感觉有些忘了。果然,没有通过消化和整理的知识是不牢靠的,趁着还没全完忘掉的时候来把这些方法总结一下,也算是复习了。
替换法(Substitution method)
替换法的基本步骤:
- 假设
- 通过数学归纳法证明假设
- 处理常数项
这个方法的关键在于「假设」,因为假设会到过大或者过小的范围。过小的范围可以在证明时被发现,因为它无法被证明;而过大的范围则难以被发现,因为它是正确的,只不过是不够精确而已。那怎么样得到一个比较精确地假设呢?这就可以使用递归树法。
递归树法(Recursion-tree method)
这种方法比较直观,而他的结果也不是很准确,但是这个结果可以被拿到替换法中进行验证。
这种方法的的大致思路是这样的:把递归运算用树的结构表示出来,然后通过计算和观察树德每一层的运算时间来推导出这个算法的共运算时间。
比如分析:T(n) = T(n/4) + T(n/2) + n^2 这个递归算法,我们可以把它表示为:
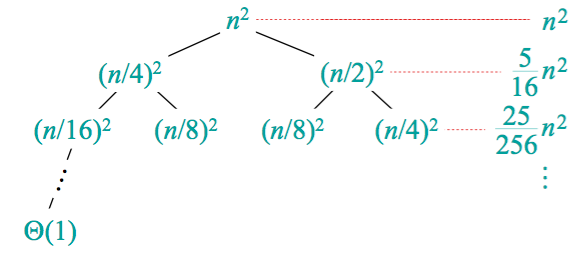
那么它的总运算时间可以表示为:n^2 * (1 + 5/16 + (5/16)^2 + (5/16)^3 + …) = n^2 * (16 / 9);用渐进分析的符号可以表示为 Ɵ(n^2)。
主定理法(The master method)
这种方法的是根据三种已经通过证明的情况来分析递归算法,这三种情况可以在 CLRS 这本书中查到,在这儿就不一一列举出来了。但是主定理法只适用于分析下面这种其形式的递归算法:
T(n) = a * T(n/b) + f(n);其中:a ≥ 1, b > 1, f(n) 是渐进为正的(aysmptotically positive)。